Answer:
Part a:
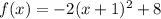
Part b: Maximum value
Explanation:
Part a.
The given function is
 .
.
We need to complete the square to obtain the vertex form
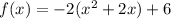
Add and subtract the square of half the coefficient of x.
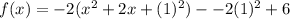
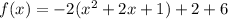
The quadratic trinomial within the parenthesis is now a perfect square
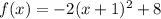
The vertex form is
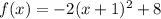
Part b
Comparing
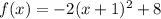 to
to
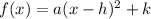 , we have a=-2.
, we have a=-2.
Since a is negative the vertex is a maximum point.
Hence the function has a maximum value