Question

Help with Algebra! Completing the square!

Answer 1

B. First off , standard form of a 2nd degree equation is Ax^2 + Bx + C. So look at the coefficient of Ax^2 which is -2.
If positive, the parabola opens up and has a minimum.
If negative, the parabola opens down and has a maximum.

A. To find the vertex (in this case maximum),
Graph the equation -OR—
make a table. — OR—
Find the zeroes and find the middle x-value
-2x^2 - 4x + 6
-2(x^2 +2x - 3 = 0
-2 (x - 1) ( x + 3)=0
x - 1 = 0. x + 3 = 0
x = 1. x = -3. So halfway would be at (-1, __).
Sub in -1 into original equation -2x^2 -4x + 6 … -2(-1)^2 -4(-1) + 6 = -2 +4 +6 = 8
So the vertex is (-1,8)

Answer 2

Part a:
`f(x)=-2(x+1)^2+8`

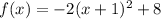
Part b: Maximum value

Explanation:

Part a.

The given function is
`f(x)=-2x^2-4x+6`.

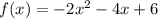We need to complete the square to obtain the vertex form

`f(x)=-2(x^2+2x)+6`

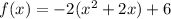
Add and subtract the square of half the coefficient of x.

`f(x)=-2(x^2+2x+(1)^2)--2(1)^2+6`

`f(x)=-2(x^2+2x+1)+2+6`

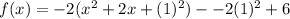
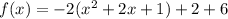
The quadratic trinomial within the parenthesis is now a perfect square

`f(x)=-2(x+1)^2+8`

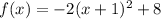
The vertex form is
`f(x)=-2(x+1)^2+8`

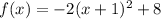
Part b

Comparing
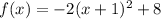`f(x)=-2(x+1)^2+8` to
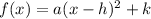`f(x)=a(x-h)^2+k`, we have a=-2.

Since a is negative the vertex is a maximum point.

Hence the function has a maximum value