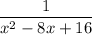Answer:
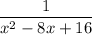
Explanation:
The expression, written in full, looks like this:
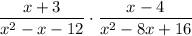
To simplify this expression, it would help us out a lot if we could factor the expressions in the denominators. Let's handle
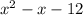 first:
first:
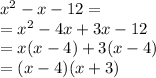
Next, we can factor
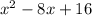 :
:
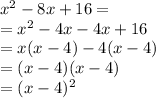
Substituting these back into our original expression, we get
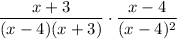
On the left, we can cancel an (x+3) in the numerator and denominator, and on the right, we can cancel an (x-4), simplifying the expression to
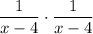
Multiplying the two together gives us the fraction
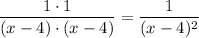
Since
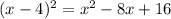 , we can rewrite this fraction in simplified form as
, we can rewrite this fraction in simplified form as