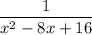Question

What is the simplified form of x plus 3 over x squared minus x minus 12 ⋅ x minus 4 over x squared minus 8x plus 16 ?

Answer 1

`(1)/(x^2-8x+16)`

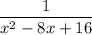
Explanation:

The expression, written in full, looks like this:

`(x+3)/(x^2-x-12)\cdot(x-4)/(x^2-8x+16)`

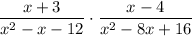
To simplify this expression, it would help us out a lot if we could factor the expressions in the denominators. Let's handle
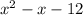`x^2-x-12` first:

`x^2-x-12=\\=x^2-4x+3x-12\\=x(x-4)+3(x-4)\\=(x-4)(x+3)`

Next, we can factor
`x^2-8x+16`:

`x^2-8x+16=\\=x^2-4x-4x+16\\=x(x-4)-4(x-4)\\=(x-4)(x-4)\\=(x-4)^2`

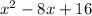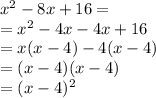
Substituting these back into our original expression, we get

`(x+3)/((x-4)(x+3))\cdot(x-4)/((x-4)^2)`

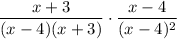
On the left, we can cancel an (x+3) in the numerator and denominator, and on the right, we can cancel an (x-4), simplifying the expression to

`(1)/(x-4)\cdot(1)/(x-4)`

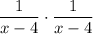
Multiplying the two together gives us the fraction

`(1\cdot1)/((x-4)\cdot(x-4))=(1)/((x-4)^2)`

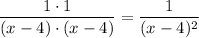
Since
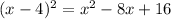`(x-4)^2=x^2-8x+16`, we can rewrite this fraction in simplified form as

`(1)/(x^2-8x+16)`