Final answer:
To find out how much will be in the account after 22 years with an annual interest rate of 8.25%, the compound interest formula
 is used, resulting in approximately $21739.63.
is used, resulting in approximately $21739.63.
Step-by-step explanation:
To calculate how much money will be in the account after 22 years with an annual interest rate of 8.25%, we will use the compound interest formula:

Where:
A is the amount of money accumulated after n years, including interest.
P is the principal amount (the initial amount of money).
r is the annual interest rate (decimal).
n is the number of times that interest is compounded per year.
t is the time the money is invested for, in years.
In this case:
P = $4400
r = 8.25% or 0.0825
n = 1 (since it's compounded annually)
t = 22 years
We plug these values into the compound interest formula:
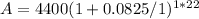
After calculating:
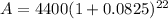
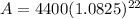
A comes out to approximately $21739.63, which is the total amount in the account to the nearest cent after 22 years.