Question

Solve the equation. Round to the nearest hundredth. Show work.


`5^(-2x-1) = 4^(4x+3)`

Answer 1

Final answer is approx x=-0.66.

Explanation:

Given equation is
`5^(-2x-1)=4^(4x+3)`.

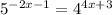Now we need to solve equation
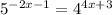`5^(-2x-1)=4^(4x+3)` and round to the nearest hundredth.

`5^(-2x-1)=4^(4x+3)`

`\log(5^(-2x-1))=\log(4^(4x+3))`

`(-2x-1)\log(5)=(4x+3)\log(4)`

`-2x \log(5)- \log(5)=4x \log(4)+3 \log(4)`

`-2x \log(5) -4x \log(4)=3 \log(4) +\log(5)`

`x=(\left(3\log(4)+\log(5)\right))/(\left(-2\log(5)-4\log(4)\right))`

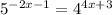
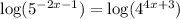
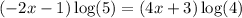
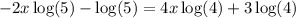
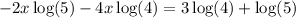
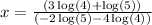
Now use calculator to calculate log values, we get:

`x=-0.65817959094`

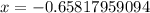
Round to the nearest hundredth.

Hence final answer is approx x=-0.66.