Answer:
The answer is ⇒ x = 0.73244
Explanation:
∵ 90^x = 27 ⇒ insert log in both sides
∴
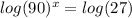
∵ 90 = 9 × 10 , 27 = 3³
∵ log(a)^b = b log(a)
∴ log(9 × 10)^x = x log(9 × 10)
∴

∵ log(a × b) = log(a) + log(b)⇒log(9 × 10) = log(9) + log(10)
∴
![x[log(9)+log(10)]=3log(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/c7xq0acdh1wo2agreohltw1dc4w199d8y9.png)
∵ log(10) = 1 , 9 = 3²
∴
![x[log(3)^(2)+1]=3log(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7jz3mlyx0l2pzhba3k2f3qjsno9h3ignnc.png)
∴
![x[2log(3)+1] = 3log(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hmfl93z2pfrtpu62ps8syke530q0ejphox.png)
∴ x = (3log3)/[2log(3)+1]
∴ x = 0.73244