ANSWER
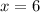
Step-by-step explanation
The given equation is
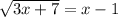
We square both sides of the equation to obtain,
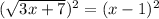
This implies that,

Rewrite in standard quadratic equation form.
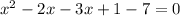
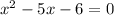
Factor
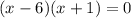
This implies that,
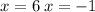
We check for extraneous solution by substituting each x-value into the original equation.
When x=-1,
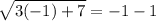
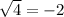
2=-2....False
Hence x=-1 is an extraneous solution.
When x=6,
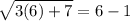
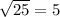
5=5 is True.
Hence x=6 is the only solution.