Question

How do you solve this ? Check for extraneous solutions

Answer 1

`x = 6`

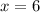
Step-by-step explanation

The given equation is

`√(3x + 7) = x - 1`

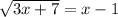
We square both sides of the equation to obtain,

`(√(3x + 7) ) ^(2) =( x - 1)^(2)`

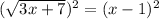
This implies that,

`3x + 7 = {x}^(2) - 2x + 1`

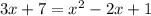
Rewrite in standard quadratic equation form.

`{x}^(2) - 2x - 3x+ 1 - 7 = 0`

`{x}^(2) -5x - 6= 0`

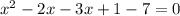
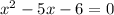
Factor

`(x - 6)(x + 1) = 0`

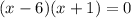
This implies that,

`x = 6 \: x = - 1`

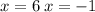
We check for extraneous solution by substituting each x-value into the original equation.

When x=-1,

`√(3( - 1)+ 7) = - 1- 1`

`√(4) = - 2`

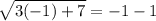
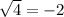
2=-2....False

Hence x=-1 is an extraneous solution.

When x=6,

`√(3( 6)+ 7) = 6- 1`

`√(25) = 5`

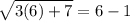
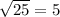
5=5 is True.

Hence x=6 is the only solution.