Question

The daily output at a plant manufacturing chairs is

approximated by the function

f(L,K) = 453KL 3/5 chairs

where L is the size of the labor force measured in hundreds

of worker-hours and K is the daily capital investment in

thousands of dollars. If the plant manager has a daily budget

of $13,000 and the average wage of an employee is $9.00

per hour, what combination of worker-hours (to the nearest

hundred) and capital expenditures (to the nearest thousand)

will yield maximum daily production?

Answer 1

Complete Question

The daily output at a plant manufacturing chairs is approximated by the function

`f(L,K) = 45\sqrt[3]{K}L^3^/^5` chairs

where L is the size of the labor force measured in hundreds

of worker-hours and K is the daily capital investment in thousands of dollars. If the plant manager has a daily budget of $13,000 and the average wage of an employee is $9.00 per hour, what combination of worker-hours (to the nearest hundred) and capital expenditures (to the nearest thousand) will yield maximum daily production?

a)200 worker-hours and $9000 in capital expenditure

b)1100 worker-hours and $3000 in capital expenditure

c)500 worker-hours and $8000 in capital expenditure

d)900 worker-hours and $5000 in capital expenditure

e)600 worker-hours and $6000 in capital expenditure

f)300 worker-hours and $10,000 in capital expenditure

Answer:

d)900 worker-hours and $5000 in capital expenditure

Explanation:

From the question we are told that

Daily output at a plant manufacturing chairs is approximated by the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5`

Daily budget of $13,000

Average wage of an employee is $9.00 per hour

a) Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to for (a)

Mathematically solving with L=200 K=9000

`f(L=200,K=9000) = (45\sqrt[3]{9000})200^3^/^5`

`f(L=200,K=9000) = 45*20.8*24`

`f(L=200,K=9000) = 22464`

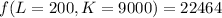
b)Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to for (b)

Mathematically solving with L=1100 K=3000

`f(L=1100,K=3000) = (45\sqrt[3]{3000})1100^3^/^5`

`f(L=1100,K=3000) = 45*14.4*66.8`

`f(L=1100,K=3000) = 43286.4`

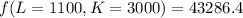
c)Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to find (c)

Mathematically solving with L=500 K=8000

`f(L=500,K=8000) = (45*\sqrt[3]{8000})*500^3^/^5`

`f(L=500,K=8000) = 45*20*41.63`

`f(L=500,K=8000) =37467`

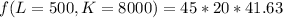
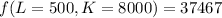
d)Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to find (d)

Mathematically solving with L=900 K=5000

`f(L=900,K=5000) = (45*\sqrt[3]{5000})*900^3^/^5`

`f(L=900,K=5000) = 45*17.09*59.2`

`f(L=900,K=5000) =45577.88`

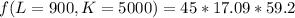
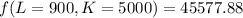
e)Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to find (e)

Mathematically solving with L=600 K=6000

`f(L=600,K=6000) = (45\sqrt[3]{6000})600^3^/^5`

`f(L=600,K=6000) = 45*18.17*46.4`

`f(L=600,K=6000) =37974`

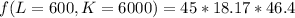
f)Generally the function
`f(L,K) = 45\sqrt[3]{K}L^3^/^5` can be use to find (e)

Mathematically solving with L=600 K=6000

`f(L=300,K=10,000) = (45*\sqrt[3]{10,000})*300^3^/^5`

`f(L=300,K=10,000) = 45*21.5*30.6`

`f(L=300,K=10,000) = 29704.2`

Therefore the function f shows maximum at L=900 K=5000

Giving the correct answer to be

d)900 worker-hours and $5000 in capital expenditure