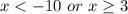Answer: OPTION D
Explanation:
Solve for x in each inequality given in the problem, as you can see below:
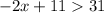
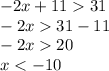
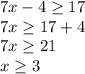
Finally you must make the union of both solutions obtained above.
Then for the first inequality you have:
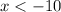
and for the second inequality you have:
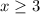
Therefore, the solution is: