Question

Solve the following compound inequality. −2x + 11 > 31 or 7x − 4 ≥ 17 Select one: A. x < -11 or x ≥ 6 B. x < 5 or x ≥ 17 C. x ≥ 3 D. x < -10 or x ≥ 3

Answer 1

The correct answer option is D. x < -10 or x ≥ 3.

Explanation:

We are given the following compound inequality and we are to solve it:

`-2x + 11 > 31` or
`7x- 4 \geq  17`

Solving them to get:

`-2x+11>31`

`-2x>31-11`

`-2x>20`

`x<-(20)/(2)`

x < -10

`7x-4\geq 17`

`7x\geq 17+4`

`x\geq (21)/(7)`

x ≥ 3

Therefore, the correct answer option is D. x < -10 or x ≥ 3.

Answer 2

Answer: OPTION D

Explanation:

Solve for x in each inequality given in the problem, as you can see below:

`-2x+11>31`

`-2x+11>31\\-2x>31-11\\-2x>20\\x<-10`

`7x-4\geq17\\7x\geq17+4\\7x\geq21\\x\geq3`

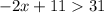
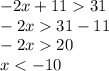
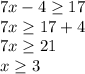
Finally you must make the union of both solutions obtained above.

Then for the first inequality you have:

`x<-10`

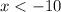
and for the second inequality you have:

`x\geq3`

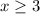
Therefore, the solution is:

`x<-10\ or\ x\geq3`