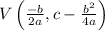Question

How do you find the vertex on a porabola​

Answer 1

The vertex on a parabola can be generalized trivially using differential calculus. See that
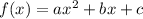`f(x) = ax^2 + bx + c` is a parabola.

Now we use the formula
`\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(x^m) = mx^(m-1)` and
`\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(f(x) + g(x)) = \frac{\mathrm{d}}{\mathrm{d}x} f(x) + \frac{\mathrm{d}}{\mathrm{d}x}g(x)` to solve this problem. We use the derivative of
`f`

`\displaystyle \frac{\mathrm{d}}{\mathrm{d}x} f(x) = \frac{\mathrm{d}}{\mathrm{d}x}(ax^2) + \frac{\mathrm{d}}{\mathrm{d}x}(bx) + \frac{\mathrm{d}}{\mathrm{d}x}(c) = 2ax + b + 0`

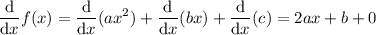
We find where
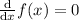`\frac{\mathrm{d}}{\mathrm{d}x} f(x) = 0`. So this is when
`\displaystyle 2ax + b = 0 \Rightarrow x = (-b)/(2a)`.

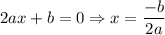This gives vertex x location. To find y location you calculate ycoordinate using f(x).

`f\left( (-b)/(2a) \right) = a\left( (-b)/(2a)\right)^2 + b\left((-b)/(2a)\right) + c = c - (b^2)/(4a)`

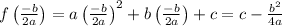
The vertex is
`V\left( (-b)/(2a), c - (b^2)/(4a) \right)`

Answer 2

A parabola ALWAYS has a lowest point like unless it would be upside down.

How to solve:

You would calculate two of the numbers to get the vertex.