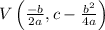The vertex on a parabola can be generalized trivially using differential calculus. See that
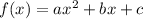 is a parabola.
is a parabola.
Now we use the formula
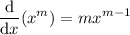 and
and
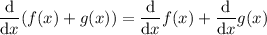 to solve this problem. We use the derivative of
to solve this problem. We use the derivative of
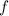
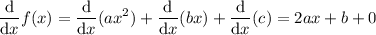
We find where
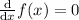 . So this is when
. So this is when
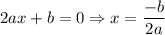 .
.
This gives vertex x location. To find y location you calculate ycoordinate using f(x).
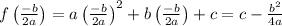
The vertex is