Question

Use the quadratic formula to find the solutions to the equation
3x^2-10x+5=0

Answer 1

Answer: x= 5-√10 / 3

x= 5 + √10/ 3

Explanation:

-(-10) +- √(-10)^2 -4 x 3 x 5 / 2x 3

x= 10 +- √100-60 / 6

x=10 +- √ 40

simplify to x = 10 +- 2√10 / 6

simplify both equations now

divide both equations by 2 which gives the answer.

Answer 2

`x=(5+ √(10))/(3)\,,\,(5- √(10))/(3)`

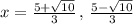
Explanation:

Let
`ax^2+bx+c=0` be a quadratic equation where a , b , c are coefficients and a ≠ 0.

Using quadratic formula, roots are given by
`x=(-b\pm √(b^2-4ac))/(2a)`

On comparing equation
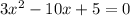`3x^2-10x+5=0` with equation
`ax^2+bx+c=0` , we get
`a=3\,,\,b=-10\,,\,c=5`

First , we will find
`b^2-4ac` :

`(-10)^2-4(3)(5)=100-60=40`

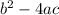So,
`√(b^2-4ac)=√(40)=2√(10)`

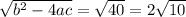
Now, using quadratic formula, we will find roots of the equation .

`\begin{align*}\displaystyle x &=(10\pm 2√(10))/(6)\\\displaystyle &=(5\pm √(10))/(3)\\\displaystyle &=(5+ √(10))/(3)\,,\,(5- √(10))/(3)\\ \end{align*}`