The function y = square root sign x is translated using the rule (x, y) → (x – 7, y + 2)to create f(x). What is the domain of f(x)? x x x x square root x

Question

The function y = square root sign x is translated using the rule (x, y) → (x – 7, y + 2)to create f(x). What is the domain of f(x)? x x > 7 x x square root x

Answer 1

Second option x

Explanation:

We have the function

`y = √(x)`

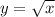
We know that the square root of a negative number has no solution in the real ones. Therefore the domain of this function is
`x > 0`

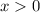
When applying the transformation:

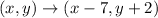`(x, y) \to (x - 7, y + 2)` we have a translation of the original function in 7 units to the right and 2 units to the top:

`f(x) = √(x-7) + 2`

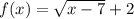
In the same way we must guarantee that
`(x-7)> 0`

Then
`x > 7`.

Therefore the domain of f(x) is x

Answer 2

a on edge

Explanation: