Question

PLEASE HELP WITH MY MATH

Answer 1

The two lines represent two equations. Their intersection represents the point for which both equations are true. So A is the solution to the system.

#

Let
`t` be the amount of time (minutes) used in a month on either plan. The first plan charges $0.18 for every minute, so you'd have to pay
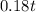`0.18t` each month. The second plan charges a flat fee of $49.95 plus $0.08 for every minute used, so that the total cost would be
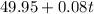`49.95+0.08t`. The second plan is preferable if its cost is less than the cost of the first plan. You want to find
`t` such that

`0.18t=49.95+0.8t`

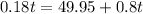
Solving gives

`0.18t=49.95+0.8t\implies0.10t=49.95\implies t=499.5`

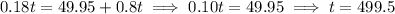
This means that after using 499.5 minutes, the second plan has a lower cost. (Just to check, if
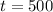`t=500`, the first plan costs
`0.18(500)=90` while the second plan costs
`49.95+0.08(500)=89.95`)

#

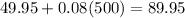Same idea as the previous problem. The daily cost for each mile
`m` with plan A is
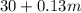`30+0.13m`, while plan B has a fixed cost of $50, independent of
`m`. The plans cost the same when

`30+0.13m=50\implies0.13m=20\implies m\approx153.8`

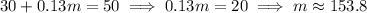
but plan B starts to save money for any mileage beyond that.