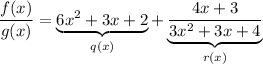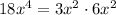 , and
, and
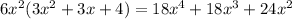
Subtracting this from
 gives a remainder of
gives a remainder of
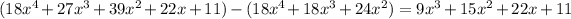
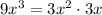 , and
, and
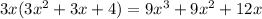
Subtracting this from the previous remainder gives a new remainder of
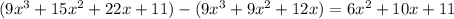
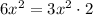 , and
, and

Subtracting this from the previous remainder gives a new remainder of
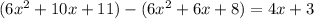
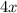 is not divisible by
is not divisible by
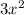 , so we're done. We ended up with
, so we're done. We ended up with