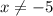For this case, we must find the inverse of the following function:
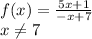
To find the inverse we follow the steps below:
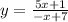
We rewrite the denominator:
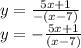
We exchange variables:
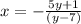
We solve for y:
We multiply on both sides of the equation by (y-7)
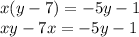
We subtract xy on both sides of the equation:
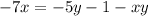
We add 1 to both sides:
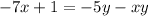
We factor for y:
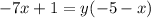
We divide both sides by (-5-x):
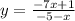
So, we have:

Answer: