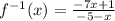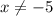Question

Find the inverse of the given function

Answer 1

For this case, we must find the inverse of the following function:

`f (x) = \frac {5x + 1} {- x + 7}\\x\\eq 7`

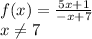
To find the inverse we follow the steps below:

`y = \frac {5x + 1} {- x + 7}`

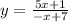
We rewrite the denominator:

`y = \frac {5x + 1} {- (x-7)}\\y = - \frac {5x + 1} {(x-7)}`

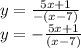
We exchange variables:

`x = - \frac{5y + 1} {(y-7)}`

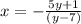
We solve for y:

We multiply on both sides of the equation by (y-7)

`x (y-7) = - 5y-1\\xy-7x = -5y-1`

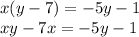
We subtract xy on both sides of the equation:

`-7x = -5y-1-xy`

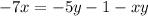
We add 1 to both sides:

`-7x + 1 = -5y-xy`

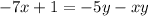
We factor for y:

`-7x + 1 = y (-5-x)`

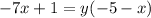
We divide both sides by (-5-x):

`y = \frac {-7x + 1} {- 5-x}`

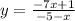
So, we have:

`f ^ {- 1} (x) = \frac {-7x + 1} {- 5-x}`

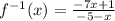
Answer:

`f ^ {- 1} (x) = \frac {-7x + 1} {- 5-x}`

`x\\eq -5`