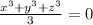Question

Mean of three numbers is 0 then what is mean of their cubes

Answer 1

`(x^3+y^3+z^3)/(3) =0`

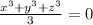
Explanation:

From the question we are told that

mean of three numbers is zero

Generally mean refers to average of number

Let

x, y, z be the three numbers with a mean of zero

T the mean of there cubes

Mathematically the mean of these three numbers is given as

`(x+y+z)/(3) =0`

`x+y+z =0`

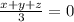
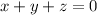
and there cubes

`(x^3+y^3+z^3)/(3) =T`

`x^3+y^3+z^3=3T`

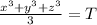
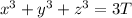
Mathematically solving the above equations by substitution method

`x+y+z =0......1`

`x^3+y^3+z^3=3T ......2`

`x=-y-z ...3`

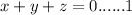
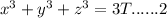
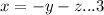
equating 3 in 2

`-y^3-z^3+y^3+z^3=3T ..... 4\\3T=0`

`T=0`

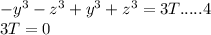
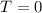
Therefore the mean of the cubes of the three number is 0

`(x^3+y^3+z^3)/(3) =0`