Question

Find the value of x to the nearest tenth.

Answer 1

Answer: The value of x is 57.8.

Step-by-step explanation: We are given to find the value of x to the nearest tenth.

We can see from the figure that

the triangle is a right-angled triangle with one of the legs measuring 11 units and the hypotenuse is 13 units in length.

For the acute angle measuring x°, the perpendicular measures 11 units.

So, we get

`\sin x^\circ=(perpendicular)/(hypotenuse)\\\\\\\Rightarrow \sin x^\circ=(11)/(13)\\\\\\\Rightarrow \sin x^\circ=0.8461\\\\\Rightarrow x^\circ=\sin^(-1){0.8461}\\\\\Rightarrow x^\circ=57.7899\\\\\Rightarrow x^\circ=57.8^\circ\\\\\Rightarrow x=57.8.`

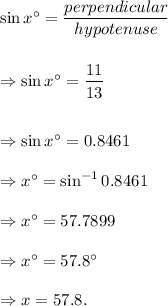
Thus, the value of x is 57.8.

Answer 2

Using the Law of Sines:

Sin(angle) = Opposite Leg / Hypotenuse

Sin(x) = 11/13

x = arcsin(11/13)

x = 57.8 degrees.