Question

Find the center and radius of the circle whose equation is x^ (2) + y ^(2) - 6x - 2y + 4 = 0

Answer 1

Explanation:

The center of a circle can be found using the equation
`(x-h)^2 + (y-k)^2 = r^2` and is (h,k) from it. Notice h and k are the opposite value as in the equation.

First write the equation in this form.

`x^2 - 6x + ( ?)+ y^2 - 2y + (?) + 4 = 0`

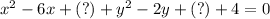
Complete the square with each variable to find what numbers should go in place of the question marks.

`(-6/2)^2 = -3^2 = 9`

`(-2/2)^2 = -1^2 = 1`

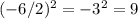
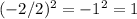
Add 1 and 9 to both sides of the equation.

`x^2 - 6x + 9 + y^2 - 2y + 1 + 4 = 1 + 9\\(x-3)^2 + (y-1)^2 + 4 = 10\\(x-3)^2 + (y-1)^2 = 6`

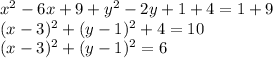
So the center is (3,1) and the radius is √6.