Question

What is the average rate of change for the sequence shown below? (-.5, 2.5), (0,3. (.5, 3.5). (1,4)

Answer 1

1

Explanation:

We are given the following sequence below and we are to find out the average rate of change for it:

(-.5, 2.5), (0,3, 0.5), (1,4)

We can find the average rate of change for this by taking any two points from this sequence and finding its slope.

Slope =
`\frac { 4 - 2.5 } { 1 - ( -0.5 ) } = 1`

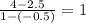
Therefore, the average rate of change for this sequence is 1.

Answer 2

The average rate of change for this sequence is 1

Explanation:

The average rate of change is calculated as the slope of the line joining the end points of the sequence.

In this case the end points are;

(-.5, 2.5) and (1,4)

We simply calculate the slope using the gradient formula;

Change in y / change in x

(4 - 2.5)/(1 - -0.5) = 1