Answer:
(a)t=10.5 seconds
(b)1764 feet
(c)t=21 seconds
Explanation:
The equation of the projectile is given by:
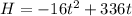
(1)The ash projectile reaches its maximum height when the slope of the line is equal to zero.
First, we find the derivative of H.
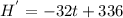
When

Divide both sides by -32
t= 10.5 seconds
(2) The maximum height occurs at the point where t= 10.5
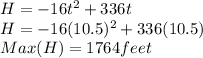
(3)The ash projectile returns back to the ground when its Height, H =0

The ash projectile returns to the ground after 21 seconds.