Hello!
The asnwer is: Cos50° ≈ 0.643
Why?
A unit circle is a cirgle with a radius equal of 1, knowing that, also know the following:
The angle is drawn passing trough the unit circle at (0.643,0.766) it means that:
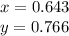
So,
Cos50° ≈ 0.643
We can prove that by following the next steps:
- If it's a unit circle,here is a right triangle with hypotenuse of 1,
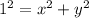
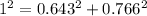
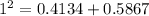
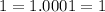
- We can determine the cosine of the angle by the following formula:
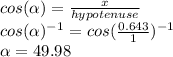
Therefore,
Cos(α)=49.98°≈50°
Also, if there is a right triangle, according to the Pythagorean Thorem:
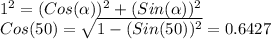
Hence,
Cos50° ≈ 0.643
Have a nice day!