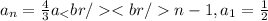Question

The explicit rule for a sequence is given

an=1/2 (4/3) n-1

Enter the recursive rule for the geometric sequence

A1=???

An=???

Answer 1

4/3an−1

Explanation:

I followed someone elses answer and it was wrong so this one is right :)

Answer 2

ANSWER


`image`

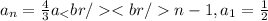
EXPLANATION

The explicit rule for the given geometric sequence is


`a_n = (1)/(2) ( (4)/(3) ) ^(n - 1)`

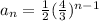
The first term of the geometric sequence can be obtained by substituting n=1.


`a_1= (1)/(2)((4)/(3) )^(1 - 1)`


`a_1= (1)/(2) ( (4)/(3) )^(0)`


`a_1= (1)/(2)`

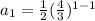
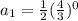
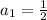
The common ratio is


`(4)/(3)`

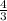
To get the subsequent terms we multiply the previous terms by


`(4)/(3)`

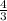
The recursive rule is therefore,


`image`