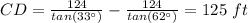Question

A man standing on a lighthouse at a height of 124 feet sights two boats directly in front of him. One is at an angle of depression of 62°, and the other is at an angle of depression of 33°. Identify the distance between the two boats. Round your answer to the nearest foot.

Answer 1

`125\ ft`

Explanation:

see the attached figure to better understand the problem

step 1

In the right triangle ABC find the length side BC

we know that

`tan(62\°)=(124)/(BC)`

`BC=(124)/(tan(62\°))`

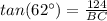
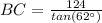
step 2

In the right triangle ABD find the length side BD

we know that

`tan(33\°)=(124)/(BD)`

`BD=(124)/(tan(33\°))`

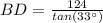
step 3

we know that

The distance between the two boats is the length side CD

`CD=BD-BC`

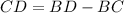
substitute the values

`CD=(124)/(tan(33\°))-(124)/(tan(62\°))=125\ ft`