Question

The sum of third and seventh terms of an AP is 20 . Find the sum of the first nine ​

Answer 1

Given:

The sum of third and seventh terms of an AP is 20.

To find:

The sum of the first nine ​ terms.

Solution:

We have, the sum of third and seventh terms of an AP is 20.

`a_3+a_7=20` ...(i)

nth term of an AP is

`a_n=a+(n-1)d`

where, a is first term and d is common difference.

`a_3=a+(3-1)d`

`a_3=a+2d` ...(ii)

`a_7=a+(7-1)d`

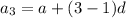
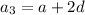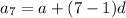
`a_7=a+6d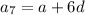` ...(iii)

Using (i), (ii) and (iii), we get

`(a+2d)+(a+6d)=20`

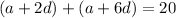
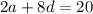`2a+8d=20` ...(iv)

Now, the sum of first n terms of an AP is

`S_n=(n)/(2)[2a+(n-1)d]`

Put n=9 to find the sum of first 9 terms of an AP.

`S_n=(9)/(2)[2a+(9-1)d]`

`S_n=(9)/(2)[2a+8d]`

`S_n=(9)/(2)[20]` [Using (iv)]

`S_n=(180)/(2)`

`S_n=90`

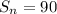
Therefore, the sum of the first 9 terms is 90.