Given:
The sum of third and seventh terms of an AP is 20.
To find:
The sum of the first nine terms.
Solution:
We have, the sum of third and seventh terms of an AP is 20.
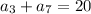 ...(i)
...(i)
nth term of an AP is
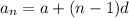
where, a is first term and d is common difference.
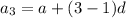
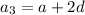 ...(ii)
...(ii)
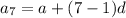
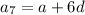 ...(iii)
...(iii)
Using (i), (ii) and (iii), we get
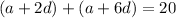
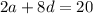 ...(iv)
...(iv)
Now, the sum of first n terms of an AP is
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2022/formulas/mathematics/high-school/hc3wqexc72lrzn5c01nbmdy9e4mhx1w0aj.png)
Put n=9 to find the sum of first 9 terms of an AP.
![S_n=(9)/(2)[2a+(9-1)d]](https://img.qammunity.org/2022/formulas/mathematics/high-school/6gusgvlcx1p2qiuvtfzm5bew931y1ckzb9.png)
![S_n=(9)/(2)[2a+8d]](https://img.qammunity.org/2022/formulas/mathematics/high-school/w8pzqv6adqzuhpezr1fpxzgfzr26xb9xqb.png)
![S_n=(9)/(2)[20]](https://img.qammunity.org/2022/formulas/mathematics/high-school/izi0jllj8necwt8th8as2fmgn9m4txkfoo.png) [Using (iv)]
[Using (iv)]
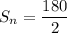
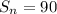
Therefore, the sum of the first 9 terms is 90.