(a) 23.8 J
The work done by the man on the block is equal to the product between the force applied by the man (F=34 N) and the displacement of the box (d=0.7 m):
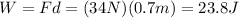
(b) 23.8 J
According to the work-energy theorem, the kinetic energy gained by the block is equal to the work done on it:
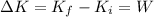
but since the block started from rest, its initial kinetic energy was zero:
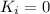 , so the final kinetic energy is simply equal to the work done:
, so the final kinetic energy is simply equal to the work done:
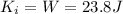
(c) 2.8 m/s
The final kinetic energy of the block is given by:
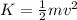
where m = 6 kg is the block's mass and v is the final speed. Solving the equation for v, we find
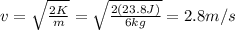
(d) 0.49 s
The impulse is defined as the product between the force applied (F) and the time taken (
 ), and it is equal to the change in momentum of the block:
), and it is equal to the change in momentum of the block:
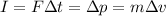
where F = 34 N, m = 6 kg, and
 is the change in velocity of the block (the initial velocity was zero). Solving for
is the change in velocity of the block (the initial velocity was zero). Solving for
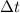 , we find
, we find
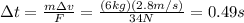
(e) 0
The man does not move, therefore the work done by the chair on the man is zero, because the displacement is zero: d = 0, so in the formula W = Fd, the result is zero.
(f) -23.8 J
According to the law of conservation of energy, energy cannot be created nor destroyed. Therefore, when the man does work on the box, he must spend some energy, and the amount of this energy must be equal to the work done on the block. Since the man has lost energy, we must also put a negative sign, so the change in internal energy of the man is -23.8 J.
(g) 16 m/s
The initial velocity of the block in the frame of reference of the train is zero:
Since the reference frame (the train) is moving to the right at speed
then the initial velocity of the block must be
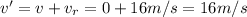
(h) 18.8 m/s
The final velocity of the block in the frame of reference of the train is 2.8 m/s, calculated at step c)
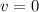
Since the reference frame (the train) is moving to the right at speed
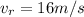
then the initial velocity of the block must be
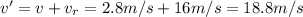
(i) 768 J
The initial kinetic energy of the block is given by:
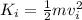
where m = 6 kg and
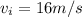 . Substituting numbers, we find
. Substituting numbers, we find

(j) 1060.3 J
The final kinetic energy of the block is given by:

where m = 6 kg and
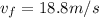 . Substituting numbers, we find
. Substituting numbers, we find
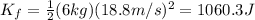
(k) 292.3 J
The change in kinetic energy is given by the difference between the kinetic energy calculated at point (j) and at point (i):
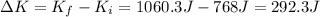
and this is greater than the same quantity in the man's reference frame.
(l) 8.52 m
The total time of the motion is
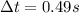 (calculated at step d). The initial velocity of the block is
(calculated at step d). The initial velocity of the block is
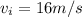 and its acceleration is given by
and its acceleration is given by
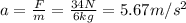
So we can calculate the displacement of the block by using
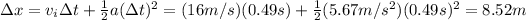
(m) 289.7 J
The work done by the man on the block in this reference frame is equal to the product between the force on the block and the displacement:
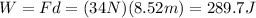
The change in kinetic energy of the block in this reference frame is
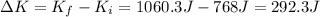
This is greater than the same quantity in the man's reference frame and it matches the ΔK in this frame (the small difference is just due to the different rounding)
(n) 7.84 m
The chair just moved by uniform motion together with the train, so its displacement is given by
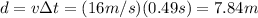
(o) 0
The chair and the man are moving together, so the chair is doing no work on the man, therefore the work done by the chair is still zero.
This is equal to the same quantity in the man's reference frame.
(p) -289.7 J
Due to the law of conservation of energy, the energy lost by the man must be equal to the work he has done. Since the work done by the man was 289.7 J, then the change in internal energy of the man must be -289.7 J.
This is greater than the same quantity in the man's reference frame.