Answer:
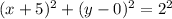
Explanation:
The standard form for the equation of a circumference is:
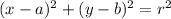
Where:
(a, b) is the center of the circumference
r is the radius
In this problem we have the equation of the following circumference, and we want to convert it to the standard form:
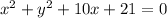
The first thing we must do to transform this equation into the standard form is to use the square completion technique.
The steps are shown below:
1. Group all the same variables:
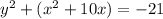
2. Take the coefficient that accompanies the variable x. In this case the coefficient is 10. Then, divide by 2 and the result elevate it to the square.
We have:
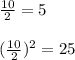
3. Add on both sides of the equality the term obtained in the previous step:
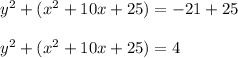
4. Factor the resulting expression, and you will get:
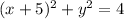
Write the equation in the standard form:
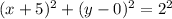
Then, the center is the point (5, 0) and the radius is r = 2.
Observe the attached image