Question

Rewrite the equation of each circle in Standard Form. Then graph.

Answer 1

(x+5)² + (y-0)² =2²

Explanation:

We have given the equation:

x²+y²+10x+21=0

We have to rewrite the equation in of circle in standard form.

The standard form of circle equation is:

(x-a)² + (y-b)² = r²

Where (a,b) is center of circle and r is the radius.

x²+y²+10 x+21=0

x²+y² +10x = -21

x² + 2(x)(5)+( 5)² + y² = -21 +(5)²

(x+5)² + y² = 4

(x+5)² + (y-0)² =2²

Comparing with standard equation we get,

The center is (5,0) and radius is 2.

Answer 2

`(x + 5) ^ 2 + (y-0) ^ 2 = 2 ^ 2`

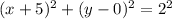
Explanation:

The standard form for the equation of a circumference is:

`(x-a) ^ 2 + (y-b) ^ 2 = r ^ 2`

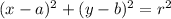
Where:

(a, b) is the center of the circumference

r is the radius

In this problem we have the equation of the following circumference, and we want to convert it to the standard form:

`x ^ 2 + y ^ 2 + 10x +21 = 0`

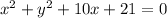
The first thing we must do to transform this equation into the standard form is to use the square completion technique.

The steps are shown below:

1. Group all the same variables:

`y ^ 2 + (x ^ 2 + 10x) = -21`

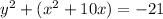
2. Take the coefficient that accompanies the variable x. In this case the coefficient is 10. Then, divide by 2 and the result elevate it to the square.

We have:

`(10)/(2) = 5\\\\((10)/(2)) ^ 2 = 25`

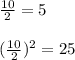
3. Add on both sides of the equality the term obtained in the previous step:

`y ^ 2 + (x ^ 2 + 10x +25) = -21 +25\\\\y ^ 2 + (x ^ 2 + 10x +25) = 4`

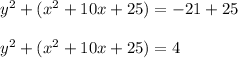
4. Factor the resulting expression, and you will get:

`(x + 5) ^ 2 + y ^ 2 = 4`

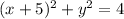
Write the equation in the standard form:

`(x + 5) ^ 2 + (y-0) ^ 2 = 2 ^ 2`

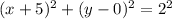
Then, the center is the point (5, 0) and the radius is r = 2.

Observe the attached image