Question

Graph the function y = 2|x|+2

Answer 1

The graph is shown as under

Explanation:

y = | x | + 2

Finding the absolute value vertex.

In this case, the vertex for y = | x | + 2 is ( 0 , 2 ) . ( 0 , 2 )

The domain of the expression is all real numbers except where the expression is undefined. In this case, there is no real number that makes the expression undefined.

( − ∞ , ∞ ) x ∈ R

For each x value, there is one y value. Select few x values from the domain. It would be more useful to select the values so that they are around the x value of the absolute value vertex.

Answer 2

Hello!

We have to remember that absolute value functions have the following form:

`f(x)=|x|\left \{ {{x,if}x\geq0 \atop {-x,if}x<0} \right.`

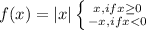
It means that there is a positive and a negative slope lines,

Let's find the information that we need to graph a absolute value function:

First:

Finding the y-intercept,

`f(0)=2(0)+2=2`

So, the y-intercept is (0,2)

Second:

Finding the two lines intercepts,

if x ≥ 0

`y=2*(x)+2=2x+2`

if x< 0

`y=2*(-x)+2=-2x+2`

Therefore,

If
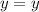`y=y` , we have that:

`-2x+2=2x+2\\2-2=2x+2x\\0=4x\\x=0`

`f(0)=-2(0)+2=2\\y=2`

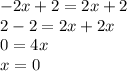
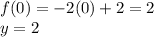
So, both lines intercepts at (0,2).