Answer:
3.21 grams
Explanation:
First we are finding the radioactive decay constant using the formula:
lambda =
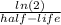
where
lambda is the radioactive decay constant.
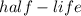 is the half life of the radioactive substance.
is the half life of the radioactive substance.
We know from our problem that Rutherfordium- 265 has a half-life of 13 hours, so let's replace the value in our formula.
lambda =
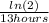
lambda = 0.0533 per hour
Now we can use the decay formula to find the remaining quantity of the substance:
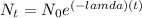
where
 is the ending amount
is the ending amount
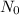 is the beginning amount
is the beginning amount
 is the time (in hours)
is the time (in hours)
We know from our problem that there is a 149g sample of Rutherfordium- 265 left at 12am on October 19th, so
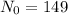 . Notice that there are exactly 3 days from 12 am October 19th to 12 am October 22nd, so we have
. Notice that there are exactly 3 days from 12 am October 19th to 12 am October 22nd, so we have
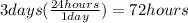 ; therefore
; therefore
 . Now we can replace all the values in our formula:
. Now we can replace all the values in our formula:
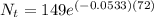

We can conclude that 3.21 grams of Rutherfordium- 265 would remain on October 22nd at 12 am.