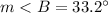Answer:
Part 1) the center is
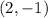 , the radius is
, the radius is
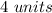
Part 2) see the procedure
Part 3)
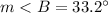
Explanation:
Part 1) we know that
The equation of a circle in center radius form is equal to
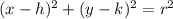
where
(h,k) is the center of the circle
r is the radius
In this problem we have
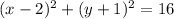
so
the center is the point
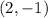
the radius is
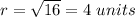
Part 2) we know that
The center of circle F' is
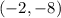 and the radius is
and the radius is
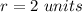
The center of circle F is
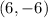 and the radius is
and the radius is
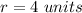
step 1
Move the center of the circle F' onto the center of the circle F
the transformation has the following rule

8 units right and 2 units up
so
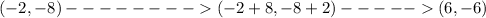
center circle F' is now equal to center circle F
The circles are now concentric (they have the same center)
step 2
A dilation is needed to increase the size of circle F' to coincide with circle F
scale factor=radius circle F/radius circle F'=4/2=2
radius circle F' will be=2*scale factor=2*2=4 units
radius circle F' is now equal to radius circle F
A translation, followed by a dilation will map one circle onto the other
Part 3) we know that
The sum of the interior angles in a quadrilateral is equal to 360 degrees
so
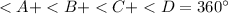
substitute the values
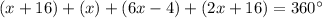
solve for x
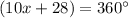
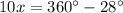
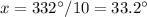
The measure of angle B is
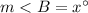
so