Is x^2 + 1/x = 4 a quadratic equations

Question

asked Apr 15, 2022 59.1k views

1 Answer

Derflo · Answer 1 · 2022-04-19T23:29:00+0000

Answer:

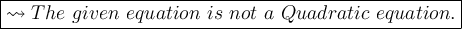
$\large\boxed{\pink{ \leadsto The \ given \ equation \ is \ not \ a \ Quadratic \ equation . }}$

Explanation:

Given equation to us is ,

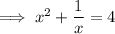
$\green{\implies x^2+(1)/(x)=4 }$

So , a equation is said to be a quadratic equation if the highest degree of the variable is 2 . On simplifying the Equation ,

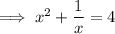
$\implies x^2 +(1)/(x)=4$

Taking x as LCM ,

$\implies (x^2.x + 1 )/(x)= 4$

Transposing x to RHS .

$\implies x^3 + 1 = 4x$

Putting all terms in LHS

$\boxed{\bf \implies x^3 - 4x - 1 = 0 }$

Since here the highest degree of the variable is 3 not 2 . So its a cubic equation and not a quadratic equation .