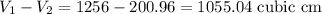Question

A cylinder has a height of 16 cm and a radius of 5 cm. A cone has a height of 12 cm and a radius of 4 cm. If the cone is placed inside the cylinder as shown, what is the volume of the air space surrounding the cone inside the cylinder? (Use 3.14 as an approximation of `pi`

Answer 1

Given:
Cylinder: height = 16 cm ; radius = 5 cm
cone: height = 12 cm ; radius = 4 cm

Volume of cylinder = 3.14 * (5cm)² * 16cm = 1,256 cm³
Volume of cone = 3.14 * (4cm)² * 12cm/3 = 200.96 cm³

Volume of air space = 1256 cm³ - 200.96 cm³ = 1,055.04 cm³

Answer 2

1055.04 cm³

Explanation:

Since, when the cone is placed inside the cylinder,

Then, the volume of the air space surrounding the cone inside the cylinder = Volume of the cylinder - Volume of the cone.

Since, the volume of a cylinder is,

`V=\pi r^2h`

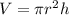
Where, r is the radius and h is the height,

Here, h = 16 cm, r = 5 cm,

So, the volume of the cylinder is,

`V_1=\pi (5)^2 (16)`

`=3.14* 25* 16`

`=1256\text{ cubic cm}`

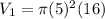
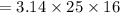
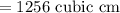
Now, the volume of a cone is,

`V=(1)/(3)\pi (R)^2 H`

Where, R is the radius and H is the height,

Here, R = 4 cm and H = 12 cm,

So, the volume of the cone is,

`V_2=(1)/(3)\pi (4)^2 (12)`

`=(1)/(3)* 3.14* 16* 12`

`=200.96\text{ cubic cm}`

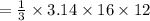
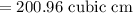
Hence, the volume of the air space surrounding the cone inside the cylinder is,

`V_1-V_2=1256-200.96=1055.04\text{ cubic cm}`