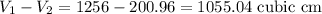Answer:
1055.04 cm³
Explanation:
Since, when the cone is placed inside the cylinder,
Then, the volume of the air space surrounding the cone inside the cylinder = Volume of the cylinder - Volume of the cone.
Since, the volume of a cylinder is,
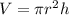
Where, r is the radius and h is the height,
Here, h = 16 cm, r = 5 cm,
So, the volume of the cylinder is,
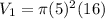
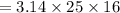
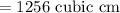
Now, the volume of a cone is,
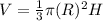
Where, R is the radius and H is the height,
Here, R = 4 cm and H = 12 cm,
So, the volume of the cone is,
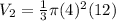
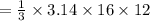
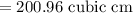
Hence, the volume of the air space surrounding the cone inside the cylinder is,