Question

Can you do this please​

Answer 1

x = 24

Explanation:

ABCD is a parallelogram.

Angle B and Angle C are adjacent (successive) angles.

Adjacent angles of a parallelogram are supplementary.

Therefore,

`(5x) \degree + (2x + 12) \degree = 180 \degree \\ \\ (5x + 2x + 12) \degree = 180 \degree \\ \\ (7x+ 12) \degree = 180 \degree \\ \\7x+ 12 = 180 \\ \\7x = 180 - 12 \\ \\ 7x = 168 \\ \\ x = (168)/(7) \\ \\ x = 24`

Answer 2

`\boxed{\pink{\sf\leadsto Value \ of \ x \ is \ 24^(\circ)}}`

`\boxed{\pink{\sf\leadsto Value \ of \ \angle C \ is \ 60^(\circ)}}`

`\boxed{\pink{\sf\leadsto Value \ of \ \angle D \ is \ 120^(\circ)}}`

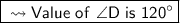
Explanation:

A parallelogram is given to us . in which m ∠ B = 5x and m ∠C = 2x + 12 ° . And we need to find x .

Figure :-

`\setlength{\unitlength}{1 cm}\begin{picture}(12,12)\thicklines\put(0,0){\line(1,0){5}} \put(5,0){\line(1,2){2}}\put(7,4){\line( - 1,0){5}}\put(2,4){\line( - 1, - 2){2}}\put(0,-0.4){$\bf A$}\put(5,-0.4){$\bf b$}\put(6.5,4.3){$\bf c$}\put(2,4.3){$\bf d$}\qbezier(4.4,0)( 4.5, 0.8)(5.22,0.54)\put(4,0.4){$\bf 5x$}\put(4.7,3.3){$\bf 2x + 12$}\end{picture}`

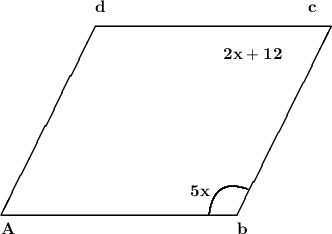
Q. no. 1 ) Find the value of x.

Here we can clearly see that ∠DCB and ∠ABC are co - interior angles . And we know that the sum of co interior angles is 180° .

`\tt:\implies \angle DCB + \angle ABC = 180^(\circ) \\\\\tt:\implies (2x + 12)^(\circ) + 5x^(\circ)=180^(\circ) \\\\\tt:\implies 7x = (180 - 12 )^(\circ) \\\\\tt:\implies 7x = 168^(\circ) \\\\\tt:\implies x =(168^(\circ))/(7) \\\\\underline{\boxed{\red{\tt\longmapsto x = 24^(\circ)}}}`

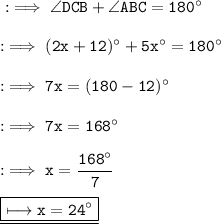
Hence the value of x is 24° .

`\rule{200}2`

Q. no. 2 ) Determine the measure of < C .

Here we can see that <C = 2x + 12 ° . So ,

`\tt:\implies \angle C = 2x + 12^(\circ) \\\\\tt:\implies \angle C = 2* 24^(\circ) + 12^(\circ) \\\\\tt:\implies \angle C = 48^(\circ) + 12^(\circ) \\\\\underline{\boxed{\red{\tt\longmapsto \angle C = 60^(\circ)}}}`

Hence the value of <C is 60° .

`\rule{200}2`

Q. no. 3 ) Determine the measure of < D .How you determined the answer .

Here we can clearly see that ∠D and ∠C are co - interior angles . And we know that the sum of co interior angles is 180° .

`\tt:\implies \angle C + \angle D = 180^(\circ) \\\\\tt:\implies 60^(\circ) + \angle D = 180^(\circ)\\\\\tt:\implies \angle D = 180^(\circ) - 60^(\circ) \\\\\underline{\boxed{\red{\tt\longmapsto \angle D = 120^(\circ)}}}`

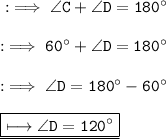
Hence the value of <D is 120° .