Answer:


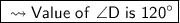
Explanation:
A parallelogram is given to us . in which m ∠ B = 5x and m ∠C = 2x + 12 ° . And we need to find x .
Figure :-
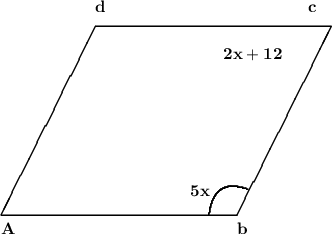
Q. no. 1 ) Find the value of x.
Here we can clearly see that ∠DCB and ∠ABC are co - interior angles . And we know that the sum of co interior angles is 180° .
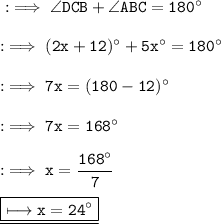
Hence the value of x is 24° .

Q. no. 2 ) Determine the measure of < C .
Here we can see that <C = 2x + 12 ° . So ,

Hence the value of <C is 60° .

Q. no. 3 ) Determine the measure of < D .How you determined the answer .
Here we can clearly see that ∠D and ∠C are co - interior angles . And we know that the sum of co interior angles is 180° .

Hence the value of <D is 120° .