Question

How long it will be in the air before bouncing

Answer 1

Given :

initial velocity = 48 m/s

`Angle of projection = \alpha  60` = 60 degrees

a. How long will it be in the air before bouncing?

Answer:

The ball's time in air before bouncing is = 8.48 seconds

Explanation:

When a ball is struck in the air at some angle, under the influence of gravitational Force it is bound to get back to the ground after covering a specific distance in some time 't'. This motion of a ball in the air under the influence of gravitational force is called 'projectile motion'.

Time of flight of a projectile motion is given as 't' where;

`t = 2(v sin\alpha  / g ) \\where g = gravitational acceleration = 9.8 ms^(-2) ,  \\ v = initial velocity of the ball and  v sin\alpha is the vertical component of velocity`

`t = 2(48* sin(60))/9.8\\t = 8.48 s`

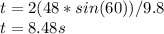
b. How far will the ball Travel before bouncing?

Answer:

The distance travelled by the ball before bouncing is 203.6 meters.

Explanation:

In this we have to find how far the ball will travel before reaching the ground and this is called the range 'R' of the projectile motion.

The distance travelled by the ball in air is it's range of the projectile motion and is calculated as :

`R = v^(2) sin 2 \alpha  /g`

`R = 48^(2) sin(2*60)/9.8\\R = 203.6 m`

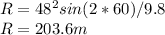
c. Determine the velocity of ball 2 seconds after it was struck?

Answer:

The velocity of ball 2 seconds after it was struck is 32.56 m/s.

Explanation:

Velocity is a vector quantity, It has two components. Horizontal and vertical. The horizontal component of velocity in a projectile motion remains constant as no force is effecting it while it is in motion. Horizontal component of velocity is given as
`v cos\alpha`

However; the vertical component of velocity changes under the influence of gravitational force and is given as :
`v sin\alpha - gt`

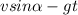
Horizontal component of velocity is always constant

Hence;
`v cos\alpha = 48(cos(60)) = 24 m/s`

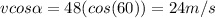
Calculating the Vertical component:

`v sin\alpha - gt = 48(sin(60)) - (9.8)(2) = 22 m/s`

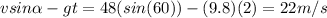
where t = 2 because we have to calculate velocity after ball has been in the air for 2 seconds.

Now;
`v = \sqrt{(vertical velocity)^(2) + (horizontal velocity)^(2)`

`v = \sqrt{22^(2) + 24^(2)  }\\ v = √(1060) \\ v = 32.56 m/s`

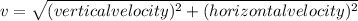
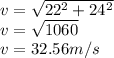
d. The most common incorrect answer is 22m/s. What has actually been calculated if this is the answer?

Answer:

If the answer calculated by a person is 22 m/s. It means that he was trying to calculate the velocity of ball after two second but only calculated the vertical component.

There is a possibility that he thought horizontal component never changes and only the vertical component changes in the air so velocity of ball after time t must be the vertical component of velocity.