Question

Paul has 9 soccer trophies, but only 6 will fit on his shelf. In how many different ways can he arrange 6 of the trophies on his shelf?

Answer 1

60,480

Explanation:

To find the number of ways that Paul can arrange his trophies, we can use the permutation formula.

The permutation formula is:

`_(n)P_(k)=(n!)/((n-k)!)`

n = 9

k = 6

Now let's put them into the formula.

`_(9)P_(6)=(9!)/((9-6)!)`

`_(9)P_(6)=(9!)/(3!)`

`_(9)P_(6)=(9!)/(3!)`

`_(9)P_(6)=60,480`

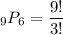
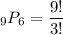
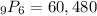
There are 60,480 different ways that Paul can arrange his trophies on the shelf.