Answer:
60,480
Explanation:
To find the number of ways that Paul can arrange his trophies, we can use the permutation formula.
The permutation formula is:
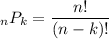
n = 9
k = 6
Now let's put them into the formula.
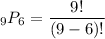
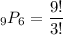
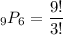
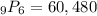
There are 60,480 different ways that Paul can arrange his trophies on the shelf.