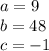Answer:
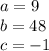
Explanation:
We know that:
In a deck of 52 cards there are 4 aces.
Therefore the probability of obtaining an ace is:
P (x) = 4/52
The probability of not getting an ace is:
P ('x) = 1-4 / 52
P ('x) = 48/52
In this problem the number of aces obtained when extracting cards from the deck is a discrete random variable.
For a discrete random variable V, the expected value is defined as:
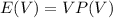
Where V is the value that the random variable can take and P (V) is the probability that it takes that value.
We have the following equation for the expected value:
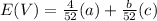
In this problem the variable V can take the value V = 9 if an ace of the deck is obtained, with probability of 4/52, and can take the value V = -1 if an ace of the deck is not obtained, with a probability of 48 / 52
Therefore, expected value for V, the number of points obtained in the game is:

So: