Question

Ming drew a triangle. The sum of the angles of the triangle is 180º.

(rest attached as images)

Answer 1

it is d. 25, 50, 105

Explanation:

bc i did on edge

Answer 2

Answer: The second matrix

If we want to write a proper matrix to represent the given system of equations, we have to arrange it in order:

`a+b+c=180`

`2a-b+0c=0`

`4a+0b-c=-5`

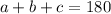
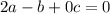
After this, we can write the matrix with the coefficients of each equation:

`\left[\begin{array}c1&1&1&180\\2&-1&0&0\\4&0&-1&-5\end{array}\right]`

Being this, the matrix that represents the measure of each angle in Ming's triangle