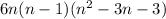Question

What is the factored form of 6n4 – 24n3 + 18n?

Answer 1

= 6n(n^3 - 4n^2 + 3)

Explanation:

6n^4 – 24n^3 + 18n

= 6n(n^3 - 4n^2 + 3)

Answer 2

The factored form is :
`6n(n-1)(n^(2)-3n-3)`

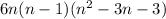
Explanation:

The given expression is :

`6n^(4) -24n^(3) +18n`

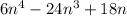
Taking out 6n out as 6n is common for all, we get

`6n(n^(3) -4n^(2) +3)`

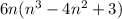
Now lets factor
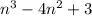`n^(3) -4n^(2) +3` by hit and trial method.

Putting n=1

Now, by hit and trial method, we put n=1,

p(n)=
`1^(3) -4(1)^(2) +3`

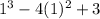
=> p(1) =
`1-4+3=0`

So, (n-1) is a factor.

Now, dividing
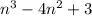`n^(3) -4n^(2) +3` by n-1 we get
`n^(2)-3n-3`

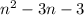
Therefore, the factored form is =
`6n(n-1)(n^(2)-3n-3)`