Answer:
Option A. Accurate. The triangles are similar and the congruent angles are listed in corresponding order
Explanation:
step 1
In the triangle TRS find the measure of angle T
Remember that
The sum of the interior angles in a triangle is equal 180 degrees
so
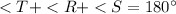
substitute the values and solve for <T
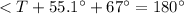
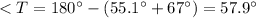
so
The triangle DAC is similar to triangle TRS by AA Similarity Postulate (The three interior angles are congruent)
The corresponding angles are
<S=<C
<R=<A
<T=<D
therefore
The triangles are similar and the congruent angles are listed in corresponding order DAC~TRS