Question

`f(x) = (2x-1)/(x^(2)-x-6 )`

Domain:
V.A:
Roots:
Y-Int:
H.A:
Holes:
O.A:

Also draw on the graph.

Answer 1

i) The given function is

`f(x)=(2x-1)/(x^2-x-6)`

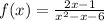
We factor to obtain

`f(x)=(2x-1)/((x-3)(x+2))`

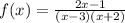
The domain is

`(x-3)(x+2)\\e0`

`(x-3)\\e0,(x+2)\\e0`

`x\\e3,x\\e-2`

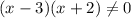
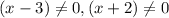
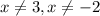
ii) The vertical asymptotes are

`(x-3)(x+2)=0`

`(x-3)=0,(x+2)=0`

`x=3,x=-2`

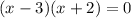
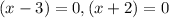
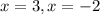
iii) To find the root, we equate the numerator to zero.

`2x-1=0`

`x=(1)/(2)`

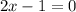
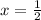
iv) To find the y-intercept, put x=0 into the function.

`f(0)=(2(0)-1)/((0)^2-(0)-6)`

`f(0)=(-1)/(-6)`

`f(0)=(1)/(6)`

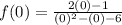
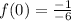
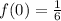
vi) To find the horizontal asymptote, we take limit to infinity.

This implies that;

`lim_(x\to \infty)(2x-1)/(x^2-x-6)=0`

The horizontal asymptote is y=0.

vii) The numerator and the denominator do not have common factors that are at least linear.

Therefore the function has no holes in it.