i) The given function is
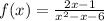
We factor to obtain
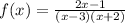
The domain is
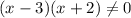
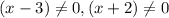
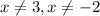
ii) The vertical asymptotes are
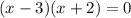
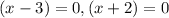
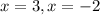
iii) To find the root, we equate the numerator to zero.
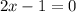
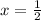
iv) To find the y-intercept, put x=0 into the function.
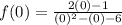
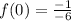
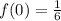
vi) To find the horizontal asymptote, we take limit to infinity.
This implies that;
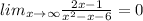
The horizontal asymptote is y=0.
vii) The numerator and the denominator do not have common factors that are at least linear.
Therefore the function has no holes in it.